Abstract
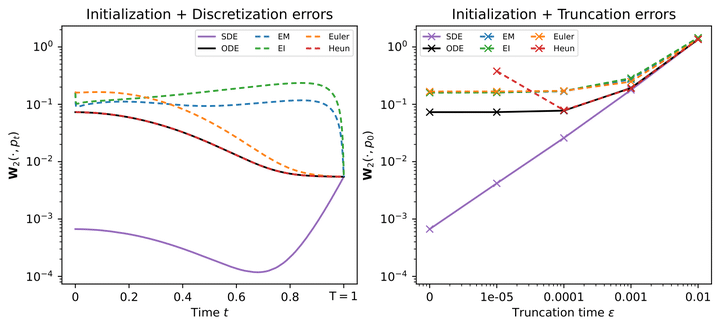
Diffusion or score-based models recently showed high performance in image generation. They rely on a forward and a backward stochastic differential equations (SDE). The sampling of a data distribution is achieved by numerically solving the backward SDE or its associated flow ODE. Studying the convergence of these models necessitates to control four different types of error: the initialization error, the truncation error, the discretization error and the score approximation. In this paper, we theoretically study the behavior of diffusion models and their numerical implementation when the data distribution is Gaussian. Our first contribution is to derive the analytical solutions of the backward SDE and the probability flow ODE and to prove that these solutions and their discretizations are all Gaussian processes. Our second contribution is to compute the exact Wasserstein errors between the target and the numerically sampled distributions for any numerical scheme. This allows us to monitor convergence directly in the data space, while experimental works limit their empirical analysis to Inception features.